문제주소 :https://programmers.co.kr/learn/courses/30/lessons/72416#
코딩테스트 연습 - 매출 하락 최소화
CEO를 포함하여 모든 직원은 팀장 또는 팀원이라는 직위를 가지고 있으며 그림에서는 팀장과 팀원의 관계를 화살표로 표시하고 있습니다. 화살표가 시작되는 쪽의 직원은 팀장, 화살표를 받는
programmers.co.kr
<문제 설명>
문제 설명
유통전문회사 카카오상사의 오너인 제이지는 새로운 사업 아이템을 구상하기 위해 전문경영인(CEO)인 프로도에게 회사의 경영을 부탁하였습니다.
"카카오상사"는 직원들을 여러 개의 팀 단위로 조직을 구성하고 있으며 아래 그림은 CEO를 포함하여 10명의 직원과 4개의 팀으로 구성되어 있는 회사 조직도를 보여주고 있습니다.

그림의 조직도는 다음과 같이 설명할 수 있습니다.
- 그림의 각 원들은 각각의 직원 1명을 표시하고 있으며, CEO를 포함하여 총 10명의 직원을 표시하고 있습니다.
- 원 안에 적힌 두 개의 숫자는 직원의 정보를 담고 있습니다. 왼쪽 숫자는 직원번호이며 직원을 식별할 수 있도록 1번부터 순서대로 발급되는 일련번호이며, 오른쪽 숫자는 해당 직원의 하루평균 매출액을 나타냅니다. 위 그림에서 1번 직원은 14원을, 9번 직원은 28원의 하루평균 매출액을 기록하고 있습니다.
- CEO를 포함하여 모든 직원은 팀장 또는 팀원이라는 직위를 가지고 있으며 그림에서는 팀장과 팀원의 관계를 화살표로 표시하고 있습니다. 화살표가 시작되는 쪽의 직원은 팀장, 화살표를 받는 쪽의 직원은 팀원을 의미합니다.
3-1. 직원번호 1번은 회사의 CEO로 고정되어 있으며, CEO는 항상 팀장이고 팀원일 수 없어 화살표를 받는 쪽이 될 수 없습니다.
3-2. 반면에 CEO를 제외한 나머지 모든 직원들은 다른 누군가로부터 정확히 1개의 화살표를 받게 됩니다.
3-3. 한 직원은 최대 2개의 팀에 소속될 수 있습니다. 만약 어떤 직원이 두 개의 팀에 소속되어 있다면, 반드시 하나의 팀에서는 팀장, 나머지 팀에서는 팀원이어야 합니다. 팀장을 겸임하거나, 두 개의 팀에서 팀원이 될 수는 없습니다. 예를들어 10번 직원은 D팀의 팀장이면서 동시에 5번 직원이 팀장으로 있는 C팀에 속한 팀원입니다.
3-4. 5번, 9번, 10번 직원은 받는 쪽의 화살표와 시작하는 화살표가 모두 있으므로 팀장인 동시에 팀원입니다.
3-5. 2번, 3번, 4번, 6번, 7번, 8번 직원은 시작하는 화살표가 없고 받는 쪽의 화살표만 있으므로 팀장이 아니며 오직 팀원입니다.
3-6. 1번 직원인 CEO는 받는 쪽의 화살표가 없고 시작하는 화살표만 있으며 항상 팀원이 아닌 팀장입니다.
3-7. 그림의 조직도에는 A, B, C, D 총 4개의 팀이 존재하며, 각각 1번, 9번, 5번, 10번 직원이 팀장 직위를 담당하게 됩니다.
"제이지"는 자신이 구상한 새로운 사업 아이템에 대해 직원들에게 설명하고자 하루 일정으로 워크숍을 계획하고 있습니다. 단, 모든 직원을 참석시킬 수 없어 아래와 같은 기준으로 워크숍에 참석할 직원들을 선발하려고 합니다.
- 워크숍에서 교육받은 내용은 전 직원들에게 공유되어야 하므로 모든 팀은 최소 1명 이상의 직원을 워크숍에 참석시켜야 합니다.
- 워크숍 기간 동안, 회사의 매출 손실을 최소화하는 것이 중요하므로 워크숍에 참석하는 직원들의 하루평균 매출액의 합이 최소가 되어야 합니다.
위 그림의 조직도에서 회색으로 색칠된 1번, 7번, 10번 직원을 워크숍에 참석시키면 모든 팀에서 최소 한 명 이상의 직원을 참석시킨 것이 되며, 해당 직원들의 하루평균 매출액의 합은 44(14+13+17)원 입니다. 10번 직원은 C팀과 D팀 모두에 속해 있으므로, 두 팀에서 모두 참석한 것으로 인정됩니다.
[문제]
직원들의 하루평균 매출액 값을 담은 배열 sales, 직원들의 팀장-팀원의 관계를 나타내는 2차원 배열 links가 매개변수로 주어집니다. 이때, 모든 팀에서 최소 한 명 이상 워크숍에 참석하면서, 참석하는 직원들의 하루평균 매출액의 합을 최소로 하려고 합니다. 그렇게 최소화된 매출액의 합을 구해서 return 하도록 solution 함수를 완성해 주세요.
[제한사항]
- sales 배열의 크기는 2 이상 300,000 이하입니다. sales 배열의 크기는 CEO를 포함한 전체 직원 수와 같습니다.
- sales 배열은 각 직원들의 하루평균 매출액을 담고 있으며, 1번 직원부터 직원번호 순서대로 주어집니다.
- sales 배열의 각 원소의 값은 0 이상 10,000 이하인 정수입니다.
- links 배열의 크기는 sales 배열의 크기 - 1 입니다. 즉, 전체 직원 수보다 1이 작습니다.
- links 배열의 각 원소는 [a, b] 형식입니다.
- a는 팀장의 직원번호, b는 a팀장이 관리하는 팀원의 직원번호이며, a와 b는 서로 다른 자연수입니다.
- 1 ≤ a ≤ sales 배열의 크기 입니다.
- 2 ≤ b ≤ sales 배열의 크기 입니다.
- 직원번호 1은 CEO로 정해져 있고 CEO는 항상 팀장으므로 b ≠ 1 입니다.
- links 배열로 만들어지는 조직도는 하나의 트리 구조 형태입니다.
- 정답으로 return 되는 값은 231 - 1 이하인 자연수임이 보장됩니다.
[입출력 예]
saleslinksresult| [14, 17, 15, 18, 19, 14, 13, 16, 28, 17] | [[10, 8], [1, 9], [9, 7], [5, 4], [1, 5], [5, 10], [10, 6], [1, 3], [10, 2]] | 44 |
| [5, 6, 5, 3, 4] | [[2,3], [1,4], [2,5], [1,2]] | 6 |
| [5, 6, 5, 1, 4] | [[2,3], [1,4], [2,5], [1,2]] | 5 |
| [10, 10, 1, 1] | [[3,2], [4,3], [1,4]] | 2 |
입출력 예에 대한 설명
입출력 예 #1
문제 예시와 같습니다.
입출력 예 #2
직원번호가 2인 직원 한 명을 워크숍에 참석시키는 것이 최선이며, 2번 직원의 하루평균 매출액은 6원입니다. 따라서 6을 return 해주어야 합니다.

입출력 예 #3
직원번호가 4, 5인 직원 두 명을 워크숍에 참석시키는 것이 최선이며, 4번, 5번 직원의 하루평균 매출액의 합은 5(1+4)원 입니다. 따라서 5를 return 해주어야 합니다.

입출력 예 #4
직원번호가 3, 4인 직원 두 명을 워크숍에 참석시키는 것이 최선이며, 3번, 4번 직원의 하루평균 매출액의 합은 2(1+1)원 입니다. 따라서 2를 return 해주어야 합니다.

<풀이법>
▒ 한줄 개념: 트리 dp ▒
어려웠던 문제입니다. 트리 dp란 개념을 이번에 처음 알게됐네요.
트리DP는 서브 트리에서 구한 해를 이용해 전체 트리의 해를 구하는 방식으로 진행이 됩니다. dp[i] = i를 루트로 하는 서브 트리의 ~~~ 와 같은 식으로 DP Table을 정의합니다.
이번 문제에서 트리 dp를 어떤식으로 적용시켰는지 간단한 예시를 들어보겠습니다.
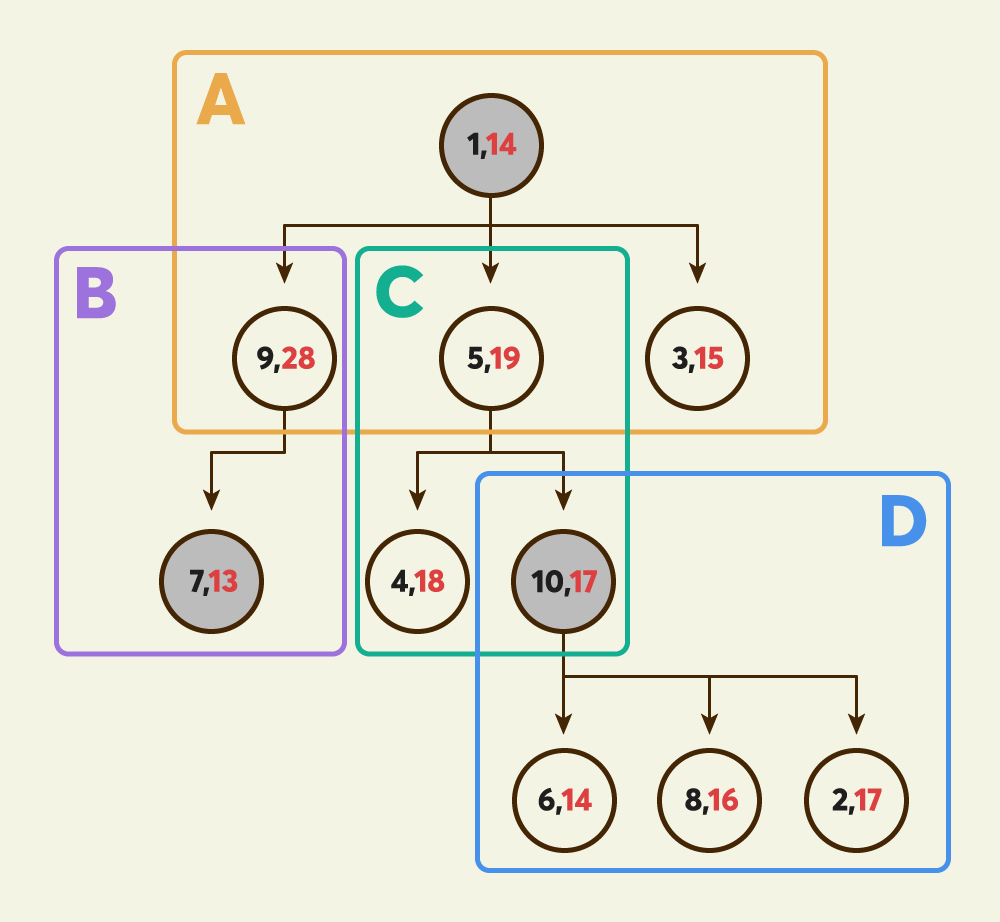
위와 같은 트리에서, 최종 목표로 하는 값은 dp[1]의 최소값입니다.
1번 노드가 무조건 루트가 되기 때문에, 별도의 계산이 필요없는 부분입니다.
dp[1]의 경우 2개의 값을 가지고 있습니다. 바로 1이 포함될 경우와, 포함될 필요가 없는 경우입니다.
팀내 한명만 포함되면 되기때문에, 같은 그룹 내 하위 노드가 하나라도 포함되어 있으면 1은 포함될 필요가 없을 겁니다. 다만 이 경우를 조건문으로 뽑아내기엔 까다롭기 때문에, 애초에 1이 포함될 경우와 포함될 필요가 없는 경우를 나눠줍니다.
따라서 dp[1]은,
dp[1][0]: 1이 포함되지 않는 경우
dp[1][1]: 1이 포함될 경우
로 나눠주게 되고, 하위 모든 노드들 또한 똑같이 2가지 경우로 나누게 됩니다.
1이 포함될 경우가 더 쉬운 경우입니다. 1이 포함되게 되면, 하위 노드가 포함 되던, 안되던 상관이 없습니다. 팀당 최소 1명이지, 1명 이상도 최소값이라면 상관이 없으니까요. 한 팀에 두명이 포함되어 있는데 최소값인 예시는, 테스트 케이스 3번의 경우입니다. (숨김글에 예시가 있습니다.)

다시 돌아가서 기본적으로 dp[1][0]과 dp[1][1]의 공통점은, 하위 서브트리의 최솟값을 가져와 더하는 것입니다. 따라서 식으로 표현하면 아래와 같습니다.
dp[1][0] = 9번의 서브트리의 최솟값 + 5번의 서브트리의 최솟값 + 3번의 서브트리의 최솟값 + a
dp[1][1] = 9번의 서브트리의 최솟값 + 5번의 서브트리의 최솟값 + 3번의 서브트리의 최솟값 + b
결과로 얻어내야하는게 무조건 최솟값이니까요. 각 하위 서브트리의 최솟값을 가져와서 더하는 부분은 같게 되고, a와 b의 차이만 있는 것입니다.
더 쉬운 dp[1][1]의 경우는 자신을 포함하는 값이므로, b = 14(자신의 값)입니다. 무조건 자신의 값이 들어가는 이유는, 어차피 팀장인 자신이 포함되면서 A 그룹에서 최소한명이 포함되야하는 조건을 만족하므로 귀찮게 조건을 따질 필요가 없는 것이지요. 따라서 dp[1][1] 식은 아래와 같이 완성됩니다.
dp[1][1] = 9번의 서브트리의 최솟값 + 5번의 서브트리의 최솟값 + 3번의 서브트리의 최솟값 + 14
=> dp[1][1] = min(dp[9][0], dp[9][1]) + min(dp[5][0], dp[5][1]) + min(dp[3][0], dp[3][1]) + 14
반면 dp[1][0]의 경우는, 조금 까다로운 면이 있는게, 두 가지 경우가 존재하기 때문입니다.
1) 자신이 포함되지 않지만, 현재 A 그룹내에 다른 한 팀원이 포함되어 있을 때
2) 자신이 포함되지 않고, 현재 A 그룹내에 어떤 다른 팀원도 포함되어 있지 않을 때
1)의 경우는 생각할 필요가 없습니다. 이미 A 그룹에서 최소한명 조건이 만족된 상태니까요. 현재 값이 최소값입니다.
반면 2)의 경우, A 그룹의 다른 팀원이 포함되어야 합니다.
식으로 만들면 아래와 같은 경우일것입니다.
1): dp[1][0] = dp[9][1] + dp[5][0] + dp[3][0]
or dp[1][0] = dp[9][0] + dp[5][1] + dp[3][0]
or dp[1][0] = dp[9][0] + dp[5][0] + dp[3][1]
위와 같은 경우, 9번이 포함되어 있거나, 5번이 포함되어 있거나, 3번이 포함되어 있습니다. 이 때는 A 그룹의 최소 한명 조건이 만족되었으므로 추가적인 계산이 필요 없습니다. 따라서 b = 0 (b값이 필요없어지는 것)입니다.
2): dp[1][0] = dp[9][0] + dp[5][0] + dp[3][0]
예제 1번의 실제 최소값의 경우입니다. 보면 최소값이 되기 위해 9번의 서브트리에서 9번이 포함되지 않고, 5번의 서브트리에서 5번이 포함되지 않으며, 3번 또한 포함되지 않습니다. 이 경우 식이 위와 같이 나오게 됩니다. 하지만 이렇게 되면 A 그룹의 최소 한명 조건이 성립되지 않습니다.
따라서, dp[9][1]이던, dp[5][1]이던, dp[3][1]이던 하나의 값은 들어가야 하는 것입니다. A 그룹의 최소 한명 조건을 맞추기 위해서요.
따라서 dp[9][0]를 dp[9][1]로 교체하던, dp[5][0]를 dp[5][1]로 교체하던, dp[3][0]를 dp[3][1]로 교체하던 처리를 해주어야합니다. 1)의 예시처럼요. 그렇게 하면, 모든 조건을 만족시킬 수 있습니다.
설명이 좀 복잡했는데, 다른 분이 설명하신 아래 동영상을 참고하시면 더 쉽게 이해하실 수 있습니다.
https://www.youtube.com/watch?v=4zzYYmnt74s
<반례>
| 입력값 〉 | [6, 5, 4, 3, 2, 10], [[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]] |
| 기댓값 〉 | 10 |
| 입력값 〉 | [2, 7, 5, 8, 10, 9, 3], [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6], [6, 7]] |
| 기댓값 〉 | 15 |
| 입력값 〉 | [6, 5, 4, 3, 2, 1], [[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]] |
| 기댓값 〉 | 9 |
<코드(Javascript)>
function solution(sales, links) {
const tree = {};
const dp = {};
links.map(link => {
const [leader, member] = link;
if(tree[leader]){
tree[leader].push(member);
}else{
tree[leader] = [member];
}
})
calcDp(tree, sales, dp, 1);
return min(dp[1]);
}
const calcDp = (tree, sales, dp, idx) => {
dp[idx] = [0, 0];
const children = tree[idx];
children.map(child => {
if(!dp[child]){
if(tree[child]){
calcDp(tree, sales, dp, child);
}else{
dp[child] = [0, sales[child-1]];
}
}
})
let checkGroup = false;
dp[idx][0] = children.reduce((acc, child) => {
if(dp[child][0] < dp[child][1]){
return acc + dp[child][0];
}else{
checkGroup = true;
return acc + dp[child][1];
}
}, 0);
dp[idx][1] = dp[idx][0] + sales[idx-1];
if(!checkGroup){
let minOffset = Number.MAX_VALUE;
children.map(child => {
const tempOffset = dp[child][1] - dp[child][0];
if(tempOffset < minOffset){
minOffset = tempOffset;
}
})
dp[idx][0] += minOffset;
}
}
const min = arr => Math.min(...arr);
더 많은 코드 보기(GitHub) : github.com/dwkim-97/CodingTest
'Programmers' 카테고리의 다른 글
| [프로그래머스] 없는 숫자 더하기 / Javascript (0) | 2021.09.14 |
|---|---|
| [프로그래머스] 입실 퇴실 / Javascript (위클리 챌린지 7주차) (0) | 2021.09.14 |
| [프로그래머스] 복서 정렬하기 / Javascript (위클리 챌린지 6주차) (0) | 2021.09.06 |
| [프로그래머스] 표 편집 / Javascript (0) | 2021.09.02 |
| [프로그래머스] 거리두기 확인하기 / Javascript (0) | 2021.09.01 |
![[프로그래머스] 매출 하락 최소화 / Javascript (+반례)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbrfjnJ%2FbtrelRo7VcU%2FAAAAAAAAAAAAAAAAAAAAAGC0yyyGdEDSMtYgUtxRjsE6A3fpsBzXSWFvp5z4N9se%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D%252BXH0Me1QQZQ0fJwuKVK1%252FpE0Yns%253D)