[프로그래머스] 블록 이동하기 / Python

문제주소 :programmers.co.kr/learn/courses/30/lessons/60063

코딩테스트 연습 - 블록 이동하기

---

<문제 설명>

문제 설명

로봇개발자 무지는 한 달 앞으로 다가온 카카오배 로봇경진대회에 출품할 로봇을 준비하고 있습니다. 준비 중인 로봇은 2 x 1 크기의 로봇으로 무지는 0과 1로 이루어진 N x N 크기의 지도에서 2 x 1 크기인 로봇을 움직여 (N, N) 위치까지 이동 할 수 있도록 프로그래밍을 하려고 합니다. 로봇이 이동하는 지도는 가장 왼쪽, 상단의 좌표를 (1, 1)로 하며 지도 내에 표시된 숫자 0은 빈칸을 1은 벽을 나타냅니다. 로봇은 벽이 있는 칸 또는 지도 밖으로는 이동할 수 없습니다. 로봇은 처음에 아래 그림과 같이 좌표 (1, 1) 위치에서 가로방향으로 놓여있는 상태로 시작하며, 앞뒤 구분없이 움직일 수 있습니다.

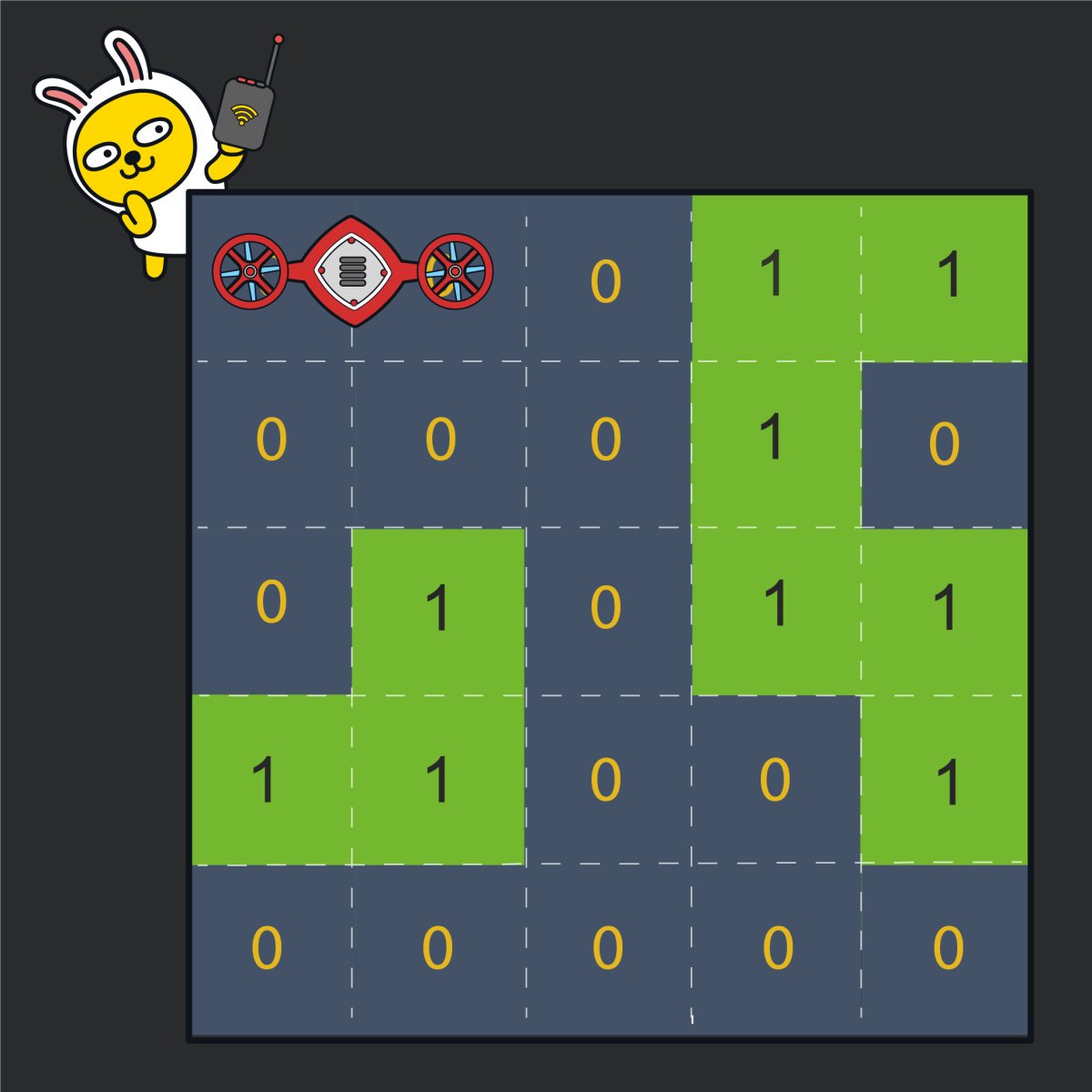
로봇이 움직일 때는 현재 놓여있는 상태를 유지하면서 이동합니다. 예를 들어, 위 그림에서 오른쪽으로 한 칸 이동한다면 (1, 2), (1, 3) 두 칸을 차지하게 되며, 아래로 이동한다면 (2, 1), (2, 2) 두 칸을 차지하게 됩니다. 로봇이 차지하는 두 칸 중 어느 한 칸이라도 (N, N) 위치에 도착하면 됩니다.

로봇은 다음과 같이 조건에 따라 회전이 가능합니다.

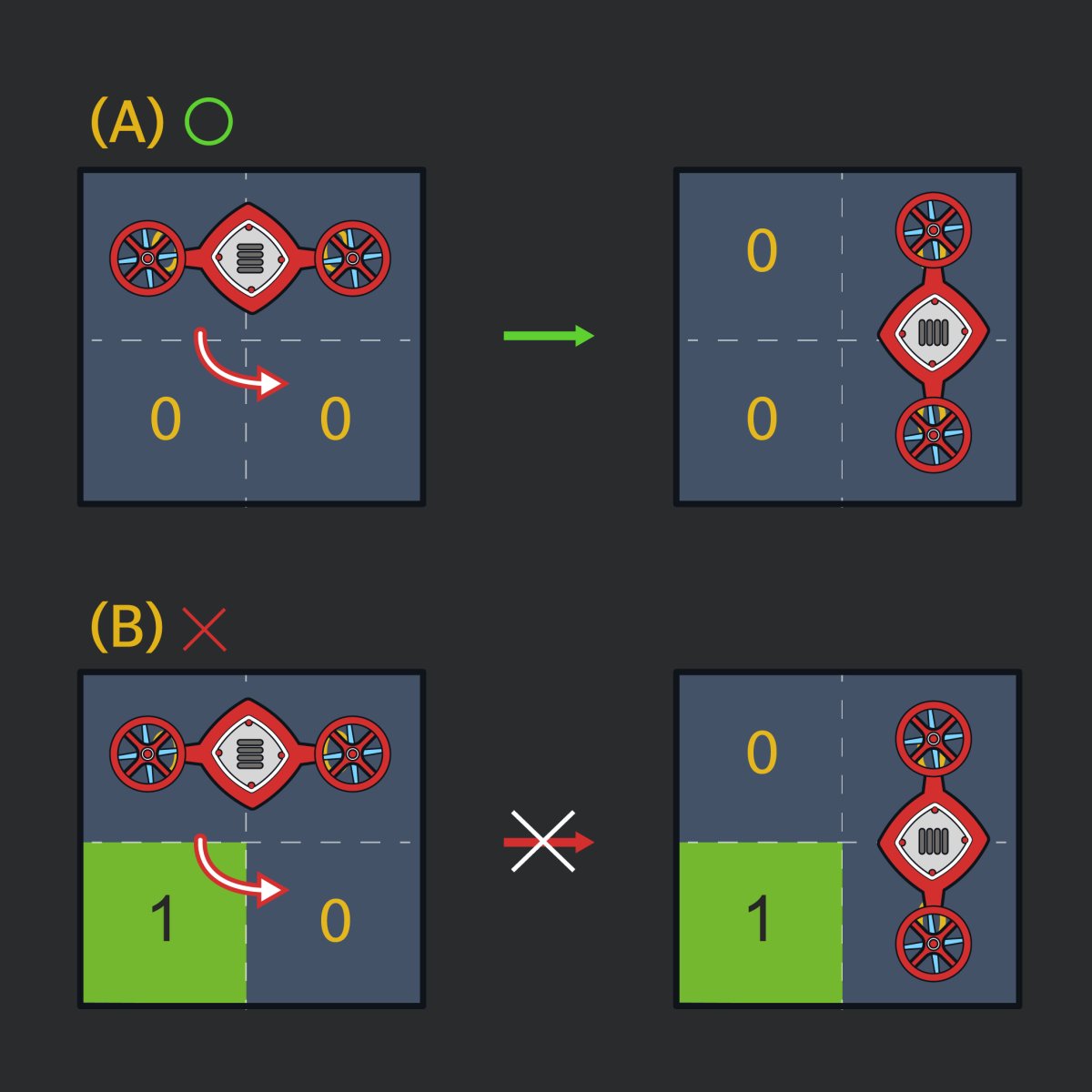
위 그림과 같이 로봇은 90도씩 회전할 수 있습니다. 단, 로봇이 차지하는 두 칸 중, 어느 칸이든 축이 될 수 있지만, 회전하는 방향(축이 되는 칸으로부터 대각선 방향에 있는 칸)에는 벽이 없어야 합니다. 로봇이 한 칸 이동하거나 90도 회전하는 데는 걸리는 시간은 정확히 1초 입니다.

0과 1로 이루어진 지도인 board가 주어질 때, 로봇이 (N, N) 위치까지 이동하는데 필요한 최소 시간을 return 하도록 solution 함수를 완성해주세요.

제한사항

• board의 한 변의 길이는 5 이상 100 이하입니다.
• board의 원소는 0 또는 1입니다.
• 로봇이 처음에 놓여 있는 칸 (1, 1), (1, 2)는 항상 0으로 주어집니다.
• 로봇이 항상 목적지에 도착할 수 있는 경우만 입력으로 주어집니다.

---

입출력 예

board                                                                  result

[[0, 0, 0, 1, 1],[0, 0, 0, 1, 0],[0, 1, 0, 1, 1],[1, 1, 0, 0, 1],[0, 0, 0, 0, 0]]

7

입출력 예에 대한 설명

문제에 주어진 예시와 같습니다.
로봇이 오른쪽으로 한 칸 이동 후, (1, 3) 칸을 축으로 반시계 방향으로 90도 회전합니다. 다시, 아래쪽으로 3칸 이동하면 로봇은 (4, 3), (5, 3) 두 칸을 차지하게 됩니다. 이제 (5, 3)을 축으로 시계 방향으로 90도 회전 후, 오른쪽으로 한 칸 이동하면 (N, N)에 도착합니다. 따라서 목적지에 도달하기까지 최소 7초가 걸립니다.

 

<풀이법>

▒ 한줄 개념: BFS ▒ 

정말 나 자신을 믿어야만 풀 수 있는 문제입니다.

사용되는 개념은 정말 단순하게도, BFS 오직 하나입니다. 다만, 모든 경우의 수를 다 만들어주어야 한다는 것이 꽤나 힘든 문제입니다. 

그나마 팁이라고 한다면 코드의 간소화나 복잡한 연산을 줄이기 위해서 2차원 배열을 1차원 배열로 변환시켜 풀었습니다.

또한 visited는 2차원 배열로 시도했다가, 경우에 따른 카운트를 전부 못할 것 같아서 (i, i+1)의 좌표값을 튜플로 갖는 리스트를 사용하였습니다.

 

결론적으로, 이 문제의 핵심은 어떠한 간소화나 코드의 효율성보다는 그냥 생각나는 대로 구현하는 것이 되겠습니다.

 

 

<코드(Python)>

def solution(board):
    N = len(board)
    new_board = []
    for i in range(N):
        for j in range(N):
            new_board.append(board[i][j])
    visited = []
    queue = [(0, 0, 1)]
    while len(queue) != 0:
        cnt, fir, sec = queue.pop(0)
        if sec == N*N-1:  # 목적지에 도달!
            return cnt
        if (fir, sec) in visited:  # 이미 방문된 적있는지 체크
            continue
        visited.append((fir,sec))  # 방문 처리
        
        if sec - fir == 1:   # 가로로 누워있는 경우
            if sec % N != N - 1 and new_board[sec + 1] == 0:
                queue.append((cnt + 1, fir + 1, sec + 1))
            if sec % N != 1 and new_board[fir - 1] == 0:
                queue.append((cnt + 1, fir - 1, sec - 1))
            if sec + N < N * N and (new_board[fir + N], new_board[sec + N]) == (0, 0):
                queue.append((cnt + 1, fir + N, sec + N))
                queue.append((cnt + 1, fir, fir + N))
                queue.append((cnt + 1, sec, sec + N))
            if sec - N > 0 and (new_board[fir - N], new_board[sec - N]) == (0, 0):
                queue.append((cnt + 1, fir - N, sec - N))
                queue.append((cnt + 1, fir - N, fir))
                queue.append((cnt + 1, sec - N, sec))
       
       else:    # 세로로 서 있는 경우
            if sec % N != N - 1 and (new_board[fir + 1], new_board[sec + 1]) == (0, 0):
                queue.append((cnt + 1, fir + 1, sec + 1))
                queue.append((cnt + 1, fir, fir + 1))
                queue.append((cnt + 1, sec, sec + 1))
            if sec % N != 0 and (new_board[fir - 1], new_board[sec - 1]) == (0, 0):
                queue.append((cnt + 1, fir - 1, sec - 1))
                queue.append((cnt + 1, fir - 1, fir))
                queue.append((cnt + 1, sec - 1, sec))
            if sec + N < N * N and new_board[sec + N] == 0:
                queue.append((cnt + 1, fir + N, sec + N))
            if fir - N > 0 and new_board[fir - N] == 0:
                queue.append((cnt + 1, fir - N, sec - N))

 

 

더 많은 코드 보기(GitHub) : github.com/dwkim-97/CodingTest