[프로그래머스] 3 x n 타일링 / Python
문제주소 :programmers.co.kr/learn/courses/30/lessons/12902#
코딩테스트 연습 - 3 x n 타일링
programmers.co.kr
<문제 설명>
문제 설명
가로 길이가 2이고 세로의 길이가 1인 직사각형 모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 3이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다
- 타일을 가로로 배치 하는 경우
- 타일을 세로로 배치 하는 경우
예를들어서 n이 8인 직사각형은 다음과 같이 채울 수 있습니다.

직사각형의 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.
제한사항
- 가로의 길이 n은 5,000이하의 자연수 입니다.
- 경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.
입출력 예
n result| 4 | 11 |
입출력 예 설명
입출력 예 #1
다음과 같이 11가지 방법이 있다.











<풀이법>
▒ 한줄 개념: 동적 계획법 ▒
n=4 에서 나타난 특이한 모양이 나머지 n에도 존재할 것이라는 것을 생각하지 못했었습니다.
홀수의 직사각형은 '절대' 채울 수 없으므로 홀수에 대해서는 return 값이 0이어야하는데, 어차피 해당 경우에 대한 테스트케이스는 존재하지 않으므로 생각할 필요가 없습니다.
우선 점화식은 다음과 같습니다.
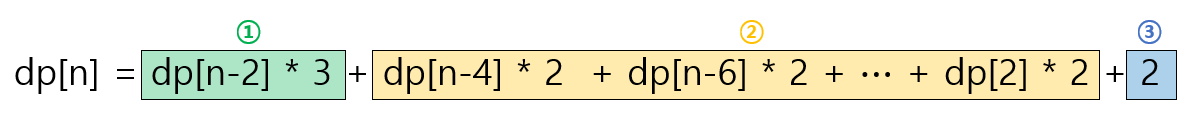
다음과 같이 점화식에는 3부분이 있는데, 그 이유는 다음과 같습니다.
① 기본 3개 종류가 추가된 것.
기본적으로 2개마다 추가할 수 있는 모양은 아래와 같이 3개가 있습니다.
이 세 가지 종류가 바로 직전의 것(dp[n-2])에 추가된 것 이 1번의 경우입니다.

② dp[2~(n-2)]에 특이한 모양이 추가된 것.
③ 현재 n에 대한 특이한 모양의 갯수
이번 문제에서는 특이한 모양이라는 경우가 존재합니다. 이 경우는 4개 이상부터 채울 수 있는데, 다음과 같이 생겼습니다. 이 특이한 모양들을 dp[2~(n-2)]까지에 추가한 경우와, 아예 현재 n에 대한 특이한 모양으로 채우는 두 가지 경우가 ②, ③이 됩니다.

dp[8]의 예시를 들면 다음과 같습니다.


<코드(Python)>
def solution(n):
mod = 1000000007
dp = [0 for i in range(n+1)]
dp[2] = 3
if n > 2:
dp[4] = 11
for i in range(6, n+1):
if i % 2 == 0:
dp[i] = dp[i-2] * 3 + 2
for j in range(i-4, -1, -2):
dp[i] += dp[j] * 2
dp[i] = dp[i] % mod
else:
dp[i] = 0
return dp[n]
더 많은 코드 보기(GitHub) : github.com/dwkim-97/CodingTest