Baekjoon

[백준9663] N-Queen / Java

개발하는 사막여우 2021. 1. 11. 15:20
반응형

TITLE

문제주소 :www.acmicpc.net/problem/9663

 

<문제 설명>

더보기

문제

N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.

N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N이 주어진다. (1 ≤ N < 15)

출력

첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.

예제 입력 1 복사

8

예제 출력 1 복사

92

<풀이법>

▒ 한줄 개념: 백트래킹 알고리즘 ▒ 

이 문제는 백트래킹 알고리즘을 사용해야하는 문제입니다. 

백트래킹 알고리즘이란 쉽게 말해 조건이 달려있는 DFS라고 생각하시면 될 것 같습니다.

DFS 방식으로 진행하되, 다음 노드에 대해 어떤 조건을 확인해서 조건에 만족하지 못할 시 해당 노드로는 진입을 하지 않는 가지치기 방식을 사용합니다.

 

백트래킹 알고리즘 간단한 예시

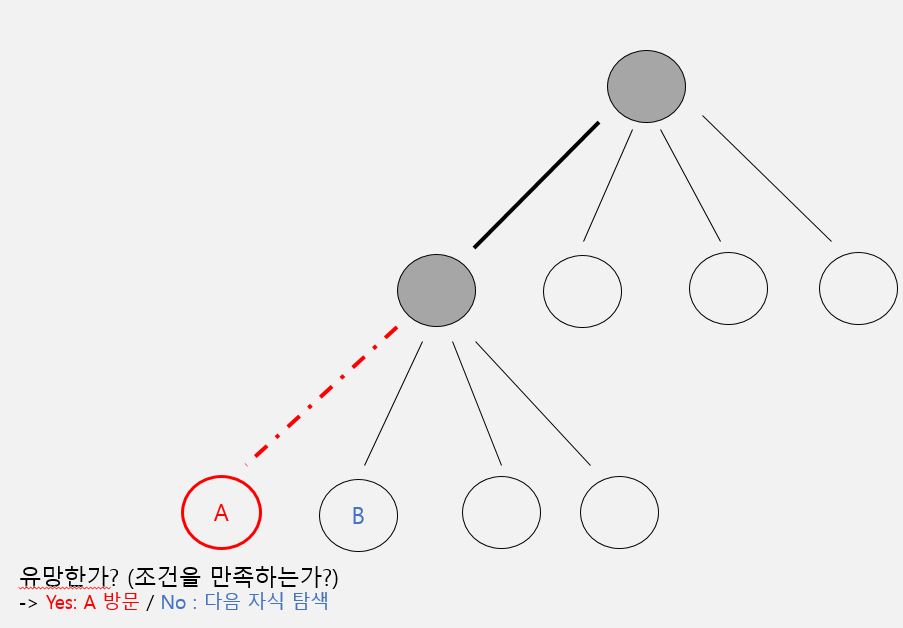
  • DFS 방식으로 탐색 -> 자식 노드(A)의 유망성(들어가도 되는가) 확인
  • 유망할 경우 -> (A)탐색
  • 유망하지 않을 경우 -> 또 다른 자식노드 (B)탐색

위와 같은 방식으로 진행되는 것을 백트래킹 알고리즘이라고 합니다.

 

이 N-Queen 문제는 N x N의 체스판에 N 개의 퀸을 서로 공격할 수 없게 두는 문제로, 백 트래킹 알고리즘의 정석과도 같은 문제라고 할 수 있습니다. 한 줄마다 퀸을 하나씩 두되, 서로의 공격범위안에 서로가 들어가 있지 않아야 하죠.

4 x 4 N-Queen의 한 해

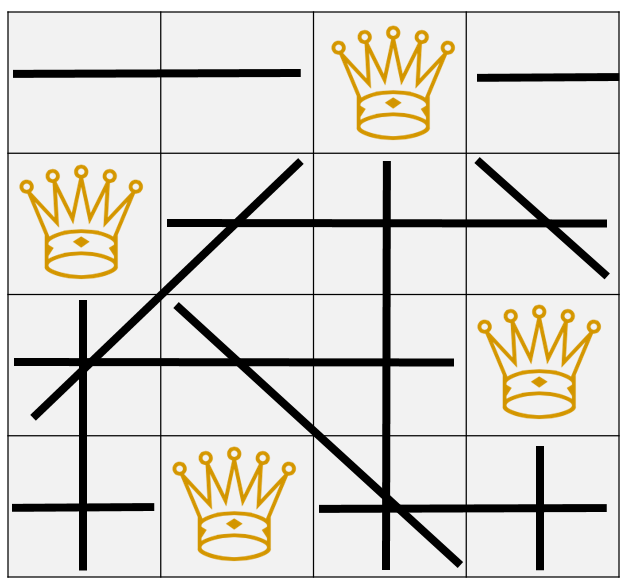
저는 재귀를 통해 각 줄을 탐색하며, 재귀로 다음 줄로 넘어가기 전 해당 위치의 유망성을 파악한 뒤, 유망성이 확인되면 재귀 탐색을 실행했습니다. 이 문제에 있어서 핵심 개념은 다음과 같습니다.

 

1. 한 줄에 하나의 퀸:

굉장히 당연한 이야기지만, 어떤 분들은 코딩을 하는데 있어서 보통 본능적으로 여러가지 예외상황을 생각하고 염두에 두기도 합니다. 이것을 생각하다보면 조건이 좀 복잡해지고 까다로워질 수 있습니다. 이 문제에서 한 줄에 퀸은 단 하나만 들어갈 수 있으므로(퀸의 공격범위는 모든 직선+대각선), 좀 더 단순하게 생각하실 필요가 있습니다.

 

2.현재 퀸들의 위치를 보여주는 1차원의 board[] 배열 :

2차원 판을 1차원으로 표현해준 것입니다. 배열의 각 인덱스는 몇 번째 row인지를 알려주는 것이고, 배열의 각 값은 몇 번째 column인지를 알려주는 것입니다. 이렇게 구현하면, 최소한의 메모리로 최대한의 표현을 할 수 있게 됩니다. 아래 그림은 위 예시를 board로 표현한 것인데, 0번 row에는 2번 column에 퀸이 위치해있으므로 board[0] = 2이고, 1번 row에는 0번 column에 퀸이 위치해있으므로 board[1] = 0입니다. 이하도 동일합니다.

board로 표현한 예시

3. 대각선 계산방법:

대각선 계산방법을 찾으려고 애를 조금 썼는데, 생각보다 매우 간단합니다. column 값의 차이와 row값의 차이가 동일하면 대각선입니다.

대각선의 예시

 

 

DFS에 위 3가지 핵심 개념들을 잘 담는다면, 저는 꽤 오래걸렸지만 바로 풀 수 있을 것이라는 생각이 듭니다.

 

<코드(Python)>

package Baekjoon;

import java.util.Scanner;

public class N_Queen_9663 {

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt(); // N 입력받음!
        int[] board = new int[N]; // Board
        int count = 0;

        for(int i = 0; i < N; i++){// 첫번째 row에 대해서는 반복문으로 재귀함수 호출
            board[0] = i;
            count += put_Queen(1, board); // count에 해당 결과값을 쌓아봅니다.
        }
        System.out.println(count);

    }

    static int put_Queen(int cur_line, int[] board){ // 퀸을 넣는 재귀함수
        int count = 0;
        int len = board.length; 
        if (cur_line == len){ // 현재 line이 board의 길이(N)과 동일하면
            return 1;         // 퀸이 다 들어간 것이니 count+1!
        }
        else{ // 다르면 아직 퀸이 들어가야할 줄(row)이 남았다.
            for(int i = 0; i < len; i++){
                board[cur_line] = i; // 일단 board에 슬쩍 넣어보고,
                if(isRight(board, cur_line, i)){ // 이 위치에 넣는게 맞는지(유망한지) 확인.
                    count += put_Queen(cur_line+1, board); // 이 위치가 맞다면 재귀 콜!
                }
            }
        }
        return count;
    }

    static boolean isRight(int[] board, int cur_line, int pos){ // 해당 위치가 맞는 위치인지 확인
        for(int b = 0; b< cur_line ; b++){ // 위쪽의 모든 퀸 위치를 반복문으로 봐서
            if(board[b] == pos) return false; // 위 퀸과 직선이면 안되고,
            if(Math.abs(b-cur_line) == Math.abs(board[b] - pos)) return false; // 위 퀸과 대각선이어도 안된다!
        }
        return true; // 모든 조건 통과했으니 pass
    }
}

 

 

더 많은 코드 보기(GitHub) : github.com/dwkim-97/CodingTest

 

 

반응형